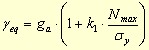Socie methods

In: local elastic-plastic strain methods->multiaxial methods

At the start, Fatemi and Socie [FS88] developed a damaging model oriented on the shear-based damage initiation:

,

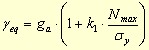where the equivalent shear strain on the critical plane was based on a combination of the maximum shear strain amplitude ga and maximum normal stress Nmax during the cycle. The shear strain was used as the variable decisive for the rain-flow decomposition. The criterion used to be based on the MSSR maximization then.

Bannantine and Socie [BS92] later focused on different modes of fatigue crack initiation and growth. They decided to extend the current model to cover also the normal mode of a crack development. Thus they build a two-step algorithm, where the Bannantine & Socie algorithm of critical plane search is applied. First, the normal mode is evaluated:

.

Here, the plane with the normal line oriented along the principal direction related to the maximum principal strain is the critical plane. The amplitude of the normal strain is mixed with the maximum normal stress in a manner similar to SWT mean stress correction. The decomposition of cycles is run with a dependance on the normal strain value. The shear mode of damaging is described by the Fatemi-Socie model:

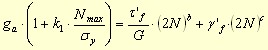
The important fact in [BS92] is the transition to the MD concept in the search for the critical plane. The authors propose their own algorithm for search over planes preferred for initiation in a particular load mode - see the Bannantine & Socie algorithm, where the planes examined are described.

The proposition of authors to evaluate the shear strains along the surface and directed into the surface only is kept in all versions of Socie's method. This reduces number of calculations because of only two different directions for resolved shear stress definition are checked for each plane.

Note 1: The maximum of the product of the normal strain amplitude and maximum normal stress is used for the normal mode in PragTic. The plane with the maximum principal normal strain can change during loading, thus the preference of the MD concept is kept to maximum.

Note 2: It is quite rare to see the complete two stage Bannantine-Socie model in a research paper. The appearance of the Fatemi-Socie shear based model is relatively frequent on the other hand. During my computations I found the dominance of the normal mode part of the computation to occur only very rarely. Based on my experimental experience, I decided to further modify the normal part of the B-S model by a parameter k2.

This change was introduced to PragTic. The modification for k2 > 1 accentuates impact of the normal part of the solution and allows a better approximation to experimental results. Nevertheless, there is no other objective reason for this change, so if you would like to keep the original formula, leave the parameters C_SOCCT or C_SOCT equal to 1.

Note 3: Note the b and c parameters in the Fatemi-Socie formula. Due to the shear load character the parameters introduced there should be bt and ct. These are nevertheless relavitely rarely available, thus Socie et al. decided to keep the parameters valid for axial loading also here. Note that the equality of the exponent parameters in both load modes is not confirmed experimentally and significant differences could be found. PragTic currently does not allow to use different exponents for different load modes, so you have to accept this reported simplification.

The implementation in PragTic offers following options:

* Socie - this is a combination of shear- and normal-mode based formulas. 

* Socie (shear v.) - original Fatemi-Socie method but in the MD variant

* Socie (normal v.) - the modified SWT parameter as introduced in the last formula, also MD solution

Nomenclature:

Decomposition - depends on the method chosen

- Complete Socie's model - (Socie method) - uses decomposition according to resolved shear strain or normal strain in dependency on the examined load mode

- Rain-flow of resolved shear variable (Socie, shear v. method) - only the two directions as mentioned above are checked

- Rain-flow of normal variable (Socie, normal v. method) - only the planes preferring the normal mode are checked in the Bannantine-Socie algorithm (i.e. with normal line deviated by 90° from surface normal line).

Elasto-plasticity

- No

Note: The Neuber-like methods allowing input of elastic stresses and strains into the fatigue damage calculation for multiaxial solution are not implemented in PragTic. The only allowed input thus is the input of transient analysis, where the elastic-plastic constitutive rules were applied in the non-linear elastic-plastic FE-solution.

Solution option

- Searched planes <0~BS algorithm, 1~globe analogy, 2~random, 3~N only>

- Number of scanned planes

- Shear component description <0~MCCM, 1~LCM, 2~by normal line> - fill in zero, please - the MCCM solution is used as default currently. Any other choice will not be reflected in the computation.

- Optimize <1~yes, 0~no>

- Negative normal stresses <0~not counted, 1~counted> - concerns behavior of the model, if the mean normal stress is below zero (and thus diminishes risk of failure). Option "0~not counted" means that only amplitude will be counted in such a case.

- Only every x-th data-point taken from load history

- Close non-closed cycles in the second run <1~yes, 0~no>

Solution variable

- Zero deviation - this value describes the maximum distance of two points on the shear load path that are claimed to be coincident. Recommended value: 1e-8

- Minimum damage – a reasonable value of damage allowing the Newton-Raphson iterative algorithm to get to the final and real value is expected. Recommended values: 1e-15 - 1e-20

- Weight of non-closed half-cycles

- Size of too small cycles (to be erased)

Material parameters

© PragTic, 2007

This help file has been generated by the freeware version of HelpNDoc